Lien vers l'index des articles de physique.
On voit que cette définition peut s'appliquer sur toutes sortes de tensions, continues, alternatives, ou quelqu'onques.
Elle est particulièrement utile naturellement dans le cas d'une tension périodique. On peut alors la calculer sur une période.
En fait la valeur efficace d'une tension ou d'un courant est utile
en cas de calculs de puissances. c'est elle que l'on retrouve dans
l'expression de la puissance active ![]() ou k est le facteur
de puissance. Dans certains cas
ou k est le facteur
de puissance. Dans certains cas
![]() .
.
On considère donc un dipole purement résistif, comme un résistor linéaire ou une résistance chaufante, dont la résistance et fixe. Par exemple on ne peut pas en toute rigueur se servir d'une ampoule à incandescence, dont la résistance dépend de la température, donc du courant qui la traverse, bien que ce dipole soit pratique pour illustrer cette grandeur comme expliqué plus bas.
Si ce dipole purement résistif a une résistance constante R, alors
en courant continu, la puissance absorbée en fonction de la tension
est en régime permanent :
En courant alternatif on a à chaque instant :
Si les deux tensions, continue constante et alternative, ont les m^emes effets, le résistor chauffera autand avec l'un qu'avec l'autre par effet joule, et absorbera en moyenne autand d'énergie dans les deux cas. On calcule donc l'énergie absorbée sur une période T pour les deux systèmes.
Tension continue constante :
![]()
Tension périodique :
![]()
On égalise, et on divise de chaque coté par la période T. R étant
une constante, on peut l'élimer.
Ce qui revient à calculer la moyenne de la tension au carré sur une période.
Pour avoir U, valeur efficace, en fonction de l'expression de u(t), il suffit donc de prendre la racine carrée de l'ensemble, ce qui revient à dire que l'on a calculé la racine carrée de la moyenne du carré.
En anglo-saxon cela se dit ``Root Mean Square'' . D'où l'abréviation
R.M.S. que l'on peut lire sur les voltmètre de qualité qui donnent
la valeur efficace vraie, et ne se contentent pas de diviser la valeur
maximale par ![]() .
.
En effet ce rapport n'est pas tout le temps valable.
On a alors l'expression de la tension suivante :
Où ![]() est la valeur maximale de la tension en volts,
est la valeur maximale de la tension en volts,
![]() est la pulsation en rad/s homogène à une vitesse de rotation, et
est la pulsation en rad/s homogène à une vitesse de rotation, et ![]() est
la phase à l'origine en radian. un choix judicieux de l'origine du
temps permet d'avoir
est
la phase à l'origine en radian. un choix judicieux de l'origine du
temps permet d'avoir ![]()
on applique alors l'equation1.
![\begin{displaymath}
U=\sqrt{\frac{\int_{0}^{T}[\hat{U}.sin(\omega.t)]^{2}.dt}{T}}\end{displaymath}](RMS_fichiers/img15.png)
On extrait les constantes de l'intégrale :
Pour intégrer on modifie l'expresion de la fonction en utilisant les relations remarquables des fonctions sinusoidales.
![]()
![]() et donc si
et donc si ![]() on a
on a
![]()
Par soustraction on en tire que
D'où , si
![]() :
:
que l'on replace dans l'expression2
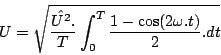
![\begin{displaymath}
U=\hat{U}.\sqrt{\frac{\left[t-\frac{\sin(2\omega.t)}{2\omega.t}\right]_{0}^{T}}{T.2}}\end{displaymath}](RMS_fichiers/img25.png)
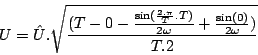
Or : ![]() et :
et :
![]()
On a donc :
soit :
CQFD
NB: cette valeur de ![]() dépend donc du fait que la fonction
u(t) est sinusoidale.
dépend donc du fait que la fonction
u(t) est sinusoidale.
avec une autre fonction, rien ne garantie que l'on retrouvera le m^eme coeficient.
Donc une tension continue n'est pas forcément constante.
Donc ne pas confondre valeur moyenne, valeur maximale, et valeur efficace.
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_subdir -split 0 -show_section_numbers /tmp/lyx_tmpdir7126dksJm8/lyx_tmpbuf0/RMS.tex
The translation was initiated by jean-christophe on 2005-08-02